Week 2 さらなる暗号技術とSNARKsとSTARKs

CircomのTIPS

コーディング

template : 回路のテンプレート。インスタンス化されることで回路のオブジェクトになる。

include : 外部のテンプレートをインポートする。

component : テンプレートをインスタンス化する。

signal input : テンプレートに入力される値。

signal output : テンプレートから出力される値。

signal : signal input の値によって変化する変数を定義する。

var : signal input の値によって変化しない変数を定義する。

<-- : シグナルに代入する。

<== : シグナルに代入しつつ、両辺が等しいという制約をR1CSに追加する。基本的に <-- ではなくこちらの使用が推奨される。

Circom特有の注意点

ハッシュ関数

circomでは値を有限体の算術回路として計算するため、ビット演算では制約が増加し、通常よりも計算量が増えます。これは使用するハッシュ関数の選定時にも重要な点で、Solidityでも使用されるkeccak-256はビット演算のため、Circomでは扱いづらいです。

そのためCircomでは有限体上で計算する以下のようなハッシュ関数が好まれます。

Poseidon: zkSNARKで最も効率的に動作。回路内での成約数を最小限に抑える設計。
MiMC: zkSNARKで効率的に動作。ラウンド数等のパラメータを選択できる。
Pedersen: 楕円曲線を使用したPedersenコミットメントに基づく。加法準同型性を持つ。

zkSNARKでは、特にPoseidonハッシュがよく利用されます。

分岐とループ

Circomのコードは算術回路などに変換された後、証明者と検証者に渡されるため、証明者から入力される signal input によって算術回路の構造を後からダイナミックに変化させることはできません。

つまり、分岐やループの条件部分など、算術回路の構造に影響を与えるような部分のCircomのコードでは、 signal の値を直接利用することができません。

例えば、if文で signal の値により分岐させたい場合には、どちらの分岐も計算され両方の和が計算されるものの、条件により分岐の片方の計算結果は0になるようにコードを書く必要があります。

これを実現するために、以下の2つの段階が必要です。

分岐ごとに、signal と比較する値が入力され、それぞれに対して0か1が出力される
前述の出力（0か1の値）と各分岐の計算結果が入力され、計算結果と前述の出力の組のどちらかの積が0となり2組の和が計算されるように出力される

前者には IsEqual や LessThan 等のテンプレートがあり、後者はシンプルな分岐の場合には容易に自身で書くこともできますが、 Mux1 テンプレート等が利用できます。

signal input in;
signal output out;
component isEq = isEqual();
isEq.in[0] <== in;
isEq.in[1] <== 7; // 比較する値
component mux = Mux1();
mux.s <== isEq.out;
mux.c[0] <== 0; // 条件と一致しないとき
mux.c[1] <== 777; // 条件と一致するとき
out <== mux.out;

Tornado Cash

Tornado Cashは、ZKによってプライバシーを保護した送金を可能にする分散型プロトコルです。

旧バージョンのTornado Cash Classicと2021年リリースのTornado Cash Novaの2種類があります。

概要（ClassicとNovaに共通）

送金するETHアドレス（Alice）と受け取るETHアドレス（Bob）の間のオンチェーン上での関係性を、第三者に分からないようにすることで、プライバシー送金を実現します。

具体的には、AliceがBobに直接送金するのではなく、Aliceがプールコントラクトに入金し、Bobがプールコントラクトから出金します。

プールコントラクトの利用者がAliceとBob以外にも多く存在し、かつ各入出金ペアの関係性が分からないとき、プライバシーを保つことができます。（ミキシング）

この状況下で、Aliceが入金したトークンをBobが出金できるようにするために、ZK（zkSNARKであるGroth16）とマークルツリーを使用しています。

Classicの特徴

Classicでは、各入金に対して秘密の文字列（プライベートノート）を生成し、出金時にそれを入力させることで、正しい出金者かを検証します。

このプライベートノートの検証にZKを使うことで、チェーン上のプールコントラクトで送金者を検証できます。

しかし、以下のような欠点もあります。

何らかの安全な方法でプライベートノートを出金者に伝える必要がある
出金のタイミングや金額を他の利用者とある程度合わせなければ、ミキシングの効果が薄れてしまう

Novaの特徴

ここでは、Classicからのいくつかの変更のうち、ミキシングに関連する部分を解説します。

Novaでは上記のようなClassicの欠点を改善するために、プライベートノートではなく、各ユーザーのアカウントごとの残高と直前の入出金額の記録（アカウントベースのUTXO）を、入出金の度に更新していくように変更されました。

AliceからBobにプライベート送金をしたい場合には、以下のフローに従います。

AliceとBobが秘密鍵を生成し、公開鍵をコントラクトに送る（アカウント作成）
Aliceは自身の秘密鍵とAliceとBobのUTXO（初回は残高０）等から、UTXOの金額等を検証するためのZKの証明を作成し、プールコントラクト上で検証と入金を行う
BobはAliceが入金したときと類似の方法（秘密鍵とUTXOの証明）で出金する

この変更により、プールコントラクト上でアカウントベースで資金を記録できるようになり、出金額を入金額と異なる金額に設定可能になったため、ミキシングの効果が高まり、より自由度の高い取引が実現しました。

リレーヤーの役割

ここまでは、ユーザーのクライアント上での秘匿化とそれがコントラクトでどのように検証・入出金されるかを確認してきました。

しかし、まだ出金側のアドレスに出金のトランザクションを実行するためのガス代が必要になるという問題があります。つまり匿名送金を受け取りたいのに、そのためには匿名ではない資金が必要になってしまうという矛盾が発生することになります。

これを解決するために、ユーザーはリレーヤーにトランザクションの実行を代理するように依頼できます。

リレーヤーは出金のトランザクション時にその金額の一部を手数料として受け取ることができます。

STARKs

以下のvitalik氏の記事を自分なりに解釈したものとなっています。 vitalik氏の記事から拝借している図もあります。ご了承ください。

https://vitalik.eth.limo/general/2017/11/09/starks_part_1.html
https://vitalik.eth.limo/general/2017/11/22/starks_part_2.html

概要

zkSNARKsは検証可能な計算やプライバシー保護型暗号通貨など、さまざまな用途に使用できる汎用の簡潔なゼロ知識証明技術である。zkSTARKsの「T」は透明性(Transparent)を意味し、zkSNARKsの課題であったTrusted Setupへの依存を解消している。また、楕円曲線やペアリング、KEAを必要とせず、ハッシュと情報理論に基づいている。これにより、量子コンピュータを持つ攻撃者に対しても安全である。

STARKs, Part I: Proofs with Polynomials

「ある多項式 $P(x)$ を知っている」ことを証明したいとする。ここでは例として $P(x)$ と $x$ は以下の性質を満たすと仮定する。

(0 \leq P(x) \leq 9), \{x \in \mathbb{N} \mid 1 \leq x \leq 10^6\}

単純な証明を考えると、 $10^6$ 点全てで $(0 \leq P(x) \leq 9)$ を確認する方法が考えられる。しかし、これは大変なのでランダムな点で検証する方法が考えられる。しかしこれもまた、サンプリングしたランダムな点において偶然 $P(x)$ と一致していた $P(x)'$ が検証を通過してしまうという問題がある。

問題の変換

まず、制約チェック多項式 $C(x)$ を導入する。 $C(x)$ は以下の性質を満たす。

\displaylines{ \begin{align} &C(x) = (x-1)(x-2) \cdots (x-9) \\ &C(x) = \begin{cases} 0 & \text{if } 0 \leq P(x) \leq 9 \\ \neq 0 & \text{if } P(x) < 0 \text{ or } P(x) > 9 \end{cases} \\ \end{align} }

ここで、「多項式 $P(x)$ を知っている」という問題は「 $C(P(x))=0$ なる $P(x)$ を知っている」という問題に変換される。

次に、 $C(P(x))$ は $(1 \leq x \leq 10^6)$ を根に持つため、 $C(P(x))$ は多項式 $Z(x)=(x-1)(x-2)\cdots (x-10^6)$ で割り切れるという事実を用いると、

「 $C(P(x))=0$ なる $P(x)$ を知っている」という問題は、「 $C(P(x)) = Z(x)D(x)$ なる $P(x)$ と $D(x)$ を知っている」という問題に変換される。 $D(x)$ は $C(P(x))$ を $Z(x)$ で多項式除算すれば求まる。

証明プロセス

問題の変換によって、以下のように証明プロセスを構築できる。

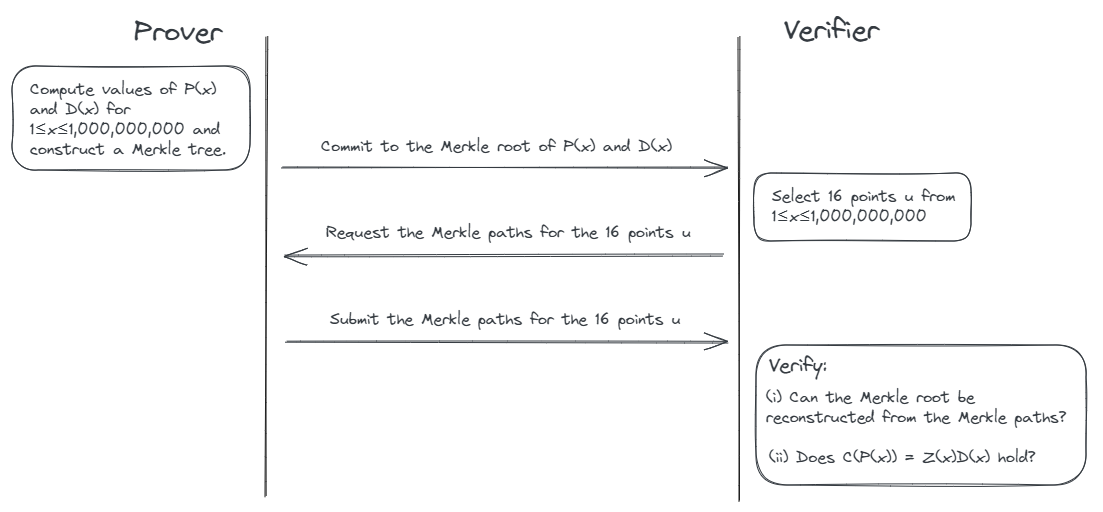
証明者は $(1 \leq x \leq 10^9)$ における $P(x)$ と $D(x)$ の値をマークルツリーにして、マークルルートを検証者にコミットする
検証者は16個の値 $u \in (1 \leq x \leq 10^9)$ を選び証明者に送る
証明者は $u$ における $P(x)$ と $D(x)$ のマークルパスを検証者に送る
検証者はマークルパスからマークルルートを構成できること、 $C(P(x)) = Z(x)D(x)$ が $u$ において成り立つことを検証する
検証が通れば、証明者は $P(x)$ を知っていることを証明できる

図で表すと以下の様になる。

更に、証明者はマークルルートをエントロピー源として $u$ を生成することで、このプロセスを非対話式にできる。これは、マークルルートを任意の値にすることが困難であるために安全に機能する。

脆弱性1

仮に攻撃者が $C(P(x)’) \neq Z(x)D(x)’$ なる $P(x), D(x)$ と次数が同じ多項式 $P(x)', D(x)'$ を偽造した場合を考える。

まず、数学的事実としてN次多項式同士の交点はたかだかN点しかない。 $C(P(x)’)$ と $Z(x)D(x)’$ は $10^7$ 次多項式なので、交点はたかだか $10^7$ 点しかない。つまり、偶然 $C(P(x)’) = Z(x)D(x)’$ が成り立つ確率は最大でも $10^7 / 10^9 = 0.01$ となる。証明プロセスでは16個の値 $u$ を使用しているので，偶然検証を通過する確率は $10^{-32}$ となる。

今回は $P(x)', D(x)'$ の次数が $P(x), D(x)$ と同じ場合を考えたため安全そうに見える。しかし、仮に $P(x)', D(x)'$ の次数が非常に大きい場合を考えると交点も非常に多くなるため、偶然 $C(P(x)’) = Z(x)D(x)’$ が成り立つ確率は $0.01$ よりも遥かに大きくなってしまう。

つまり、この攻撃を防ぐためには証明者が提供する $P(x)$ と $D(x)$ の次数に上限を設ける必要がある。

脆弱性2

次に、攻撃者が以下の様に $P(x)$ と $D(x)$ を偽造した場合を考える。

$P(x)$ の代わりに適当な値 $p$ を使う
$D(x)$ の代わりに $d=C(p)/Z(x)$ を使う

この場合、 $C(p)=Z(x)d$ は常に成り立つため検証を通過する。

つまり、この攻撃を防ぐためには証明者が提供する点の集合が、ある多項式上に存在することを検証する必要がある。

解決策

これらの脆弱性に対応するため、low-degree testingの一種であるFRIを導入する。これによって、証明者から提供された点の集合が確かにある次数未満の多項式上にあることを検証することで、上記の攻撃手法を防ぐことができる。

STARKs, Part II: Thank Goodness It's FRI-day

証明者が提供した点の集合について、それら全てが次数 $D$ 未満の同じ多項式上にあると主張することを考える。

仮に $p$ 割の点が多項式上に無い場合、この主張は $D+k$ 回の(検証者側の)クエリで $(1-p)^k$ の確率で検証を通過する。(ラグランジュ補間を使えば $D+1$ 個の点から $D$ 次多項式を作れるため)

このままでも良いが、 $D$ が大きい場合は大変なので、以下のテクニックを使って証明者・検証者の計算量を削減していく。

二変数関数

$10^9$ 個の点が次数 $10^6$ 未満の多項式 $f(x)$ 上にあるとする。

まず、 $f(x)=g(x, x^{1000})$ を満たすような二変数関数 $g(x, y)$ を見つける $(y=x^{1000})$ 。見つけ方は簡単で、 $f(x)$ の $k$ 次の項を以下の様に変換すればよい。

x^k \to x^{k \bmod 1000}y^{floor(k / 1000)}

例えば $1744x^{185423}$ という項は以下のように変換される。

1744x^{185423} \to 1744x^{423}y^{185}

この変換を用いると、次に記すように $D+k$ 回のクエリ以下で検証を行う事ができる。

証明プロセス

二変数関数を用いて以下のように証明プロセスを構築できる。

証明者は $g(x, y)$ を計算して以下の正方形を作成し、 $10^9$ × $10^9$ 個の値をツリーにしてマークルルートをコミットする(正方形の対角線は $f(x) = g(x, x^{1000})$ の値を意味する)
検証者は行と列を数十個指定して、各行/列に対して $1000 + k$ 個の点を要求する (このうち一つは対角線上の点)
証明者は指定された点における $g(x, y)$ の値とマークルパスを提出する
検証者はマークルパスが正しいこと、各行/列の点が次数<1000の多項式上にあることを検証する
検証が通れば、証明者は提供した点の集合がある次数未満の多項式上にあることを証明できる

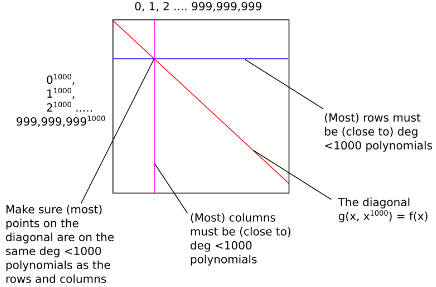
$f(x)$ は次数 $10^6$ 未満の多項式であったが、行と列を指定( $x$ or $y$ を固定)することで $f(x) = g(x, y)$ を次数1000未満の多項式にすることができた。

例として30行, 30列, 1010点を指定すれば、60600点にアクセスすることになり、元の $10^6$ 未満のクエリよりも大幅に少なくなっていることが分かる。

更なる効率化1

フェルマーの小定理より、有限体 $F_p$ において $p-1$ が $k$ の倍数ならば、関数 $x \to x^k$ は $(p-1)/k+1$ 通りの値のみ出力することが知られている。

この数学的事実を基に更なる効率化を行う。まず、有限体の位数として $10^9$ より大きく、素数であり、 $p-1$ が $1000$ の倍数である $p=1,000,005,001$ を選ぶ。このとき、関数 $x \to x^{1000}$ は $1,000,006$ 個の出力しか持たない。

これを利用すると、正方形の列方向の値の個数は、 $10^9$ から $1,000,006$ に減少する。つまり、計算の複雑さは $10^{18}$ から $10^{15}$ に減少する。

この図を見ると、列方向が有限体で記述されているために、対角線がループしていることに気づく。つまり、一つの行に対角線上の点が1000点含まれているということである。この事実を利用すると、証明者は対角線上の値のみコミットすれば良く、検証者はある一組の行と列を指定すれば十分に証明を満足する結果が得られる。

ここら辺の理解が非常に難しいと思います。メンターの方によれば、「元の多項式 $f(x)$ を $(1 \leq x \leq 10^9)$ の範囲で評価した結果(対角線)をコミットしておけば、任意の $y$ (行)での値を1000個の $x$ (列)で評価した結果と見做すことができる」ということみたいです。

更なる効率化2

先ほどの考え方を導入すると、証明プロセスは以下の様になる。

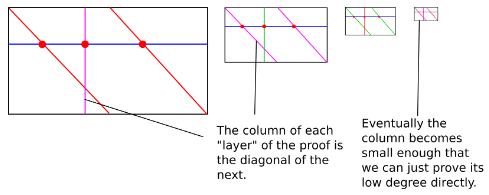
証明者は対角線の値のみ計算してコミットする
検証者は一組の列と行を指定する
証明者は列の値と、行の対角線上の1000点を提出する
検証者は列の値から次数1000未満の多項式を構成できること、対角線上の1000点から次数999の多項式を構成できること、列と行の交点が多項式上にあることを検証する
検証が通れば、証明者は提供した点の集合がある次数未満の多項式上にあることを証明できる

よって、計算の複雑さは $10^{15}$ から $10^{9}$ に減少する。

更なる効率化3

$f(x) = g(x, x^{1000})$ ではなく、 $f(x) = g(x, x^{2})$ を採用すると、行方向は次数2の多項式、列方向は次数 $D/2$ の多項式となる。

列方向の多項式に同様の操作を再帰的に繰り返すと、計算の複雑さは以下の様になり、更なる効率化を達成できる。

D + \frac{D}{2} + \frac{D}{4} + \cdots = 2D

PreviousWeek 1 NextWeek 5 Frontier

Last updated 8 months ago

signal input in; signal output out; component isEq = isEqual(); isEq.in[0] <== in; isEq.in[1] <== 7; // 比較する値 component mux = Mux1(); mux.s <== isEq.out; mux.c[0] <== 0; // 条件と一致しないとき mux.c[1] <== 777; // 条件と一致するとき out <== mux.out;